Exponent Law - Part 2

Lesson Objective

This lesson shows you the basics behind the next three exponent laws. You will learn how these laws are derived...

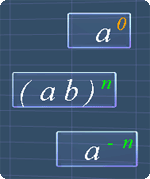
Study Tips

Tip #1

Let's recall the first three exponent laws before proceeding further. The picture below shows the 1^st law. Here is an example on how to use it:

       6a¹⁰ x 3a^-5= 6 x 3 x a¹⁰ x a^-5
                       = 18 x a^{10 + (-5)}
                       = 18 x a^{10 -5}
                       = 18a⁵

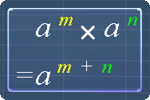
Tip #2

As for the 2^nd law of exponent, the picture below shows the law. Here is an example on how to use it:

       6a¹⁰ ÷ 3a^-5 = 2a¹⁰ ÷ a^-5
                       = 2a^{10 - (-5)}
                       = 2a^{10 + 5}
                       = 2a¹⁵

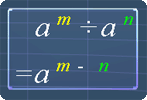
Tip #3

Finally, for the 3^rd law of exponent, the picture below shows the law. Here is an example on how to use it:

          2(a¹⁰)^-5= 2 x a^{10 x (-5)}
                       = 2a^-50

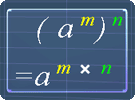
Tip #4

You may come across terms like a¹ or 2¹. These terms simply mean that:

                              a¹ = a
                              2¹ = 2

We can explain them using the following observation:

                             2³ = 2 x 2 x 2
                             2² = 2 x 2
            Therefore:   2¹ = 2

Now, watch the following math video to learn the next three laws.

Math Video

Click play to watch video

Sponsored Links

Math Video Transcript

00:00:01.060
This lesson is a continuation from part 1 of the Exponent Laws.

00:00:07.020
To emphasize, it is very important to understand the logic behind these laws before you use them.

00:00:13.110
The laws that you are going to learn can be derived from the first three laws in part 1. So, they are not completely new.

00:00:22.050
Let's start, consider this term, bracket 2 multiply by 3 , to the power of 4.

00:00:30.060
Now, we can break this term into four parts of bracket 2 multiply by 3.
 
00:00:36.220
We can see that 2 multiply by 2, multiply by 2, multiply by 2, gives 2 power of 4.

00:00:45,070
Similarly, 3 multiply by 3, multiply by 3, multiply by 3, gives 3 power of 4

00:00:54.110
Now, notice this, this term bracket 2 multiply by 3 to the power of 4 is equals to, 2 to the power of 4 multiply by 3 to the power of 4. 

00:01:04.210
With this observation, we can now formulate an exponent law. 

00:01:09.160
Let's first replace these numbers with alphabetical letters.  This gives bracket  'a' multiply by 'b' to the power of n. 

00:01:19.140
By referring to this, we can also see this term, bracket 'a' multiply by 'b' to the power of N is equals to, 'a' to the power of 'n' multiply by 'b' to the power of n. 

00:01:33.100
So, we have another law of exponent. Bracket 'a' multiply 'b' to the power of 'n' is equals to, 'a' to the power of 'n'  multiply b' to the power of 'n'. 

00:01:46.060
Let's take a look at the next law of exponent. For us to understand this law, let's consider dividing 2 to the power of 3 with 2 to the power of 3.

00:01:56.200
Now, using the second exponent law, we can see that, this term is equals to, 2 to the power of 3 minus 3.

00:02:08.090
Three minus by three is 0. So, now we have 2 to the power of 0.

00:02:14.240
Alright, let's calculate this term using another way. We can see that 2 to the power of 3 divides by 2 to the power of 3 is equals to, 8 divides by 8.   

00:02:26.200
Now, 8 divides by 8 gives 1.

00:02:30.220
From here, we can see something interesting.  Since all these terms are equal to each other, we can say that, 2 to the power of zero is equals to 1.

00:02:41.230
With this observation, we can now formulate an exponent law. 

00:02:46.200
Let's first replace this number, '2' with 'a'. This gives 'a' to the power of zero.

00:02:54.160
By referring to this, we can deduce that, 'a' to the power of zero is equal to 1.

00:03:02.000
So, here we have another law of exponents. 'a' to the power of zero equals to 1.

00:03:02.000
Let's take a look at the next law of exponent. For us to understand this law, let's consider this term, 1 divides by 2 to the power of 3.

00:03:20.030
Now, notice the number 1, at the numerator. Using this exponent law, 'a' to the power of zero equals to 1, we can rewrite 1 as, 2 to the power of 0.

00:03:36.120
Now, using the second law of exponents, 2 to the power of 0 divides by two to the power of 3 is equals to, 2 to the power of 0 minus 3.

00:03:50.100
0 minus 3 gives negative 3. So now we have,  2 to the power of negative 3.

00:03:58.150
Again, we can see something interesting. If we observe carefully, since all these terms are equal, we can see that 2 to the power of negative 3 is equals to 1 divides by 2 to the power of 3.

00:04:12.090
Let's rewrite these two terms here.


00:04:15.240
With this observation, we can now formulate an exponent law. 

00:04:20.140
Let's first replace these numbers with alphabetical letters. This gives 'a' to the power of negative 'n'.

00:04:29.160
By referring to this, we can deduce that, 'a' to the power of negative 'n' is equals to, 1 divides by 'a' to the power of 'n'.

00:04:41.080
Finally, we have another law of exponents. 'a' to the power of negative 'n' equals  1 divides  'a' to the power of 'n'.

00:04:50.160
That is all for this lesson. The next lesson will show you some examples on using what you have learn in this lesson.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on exponent laws - Part 2 or pick your choice of question below.

Question 1 on the basics of the next three exponent laws

More Lessons

Here are more lessons that you might be interested:

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons