Using the slope formula to prove that a point is on the line AB

by Mary
(China)

Question

Prove that the straight line passing through A(2,3) and B(-4,-6) passes through the origin.

Answer

Let's do a quick sketch of the points, A(2,3) and B(-4,-6).This is shown in the picture below: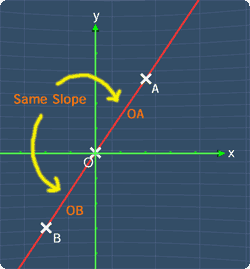
By observing carefully, we can see that if the origin O(0,0) is located on the line AB, the slope of the line segment OA is the same as the slope of the line segment OB. Hence, we can prove this question by showing that the slope of the line OA and OB are the same.

To calculate the slope of a line, we can use the slope formula:
Let's find the slope of the line OA first. To do so, we let:

O(0,0) = (x₁,y₁) and
A(2,3) = (x₂, y₂) 

Substituting the above values into the slope formula, we have:

m = (y2 -y1)/(x2 - x1)
    = (3 -0)/(2 -0)
    = 3/2
    = 1.5

Similarly, we now find the slope of the line OB. To do so, we let:

O(0,0) = (x₁,y₁) and
B(-4,-6) = (x₂, y₂) 

Substituting the above values into the slope formula, we have:

m = (y2 -y1)/(x2 - x1)
    = (-6 -0)/(-4 -0)
    = (-6)/(-4)
    = 6/4
    =1.5

We can see that the line segment OA and OB have the same slope (m = 1.5). Therefore, we proved that the line AB passes through the origin...