Compound Interest Formula

Lesson Objective

In this lesson, we will learn about the basics behind compound interest formula...

Study Tips

Tip #1

The compound interest formula is given below:

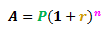
Where:

A is the total amount of money (including interest) after n years
P is the principal (the amount money borrowed or invested)
r is the interest rate (per year or per annum)
n is the loan or investment duration in years

The math videos below will explain more on this formula. You can see the examples on using this formula here.

Math Video

Video on Figuring Compound Interest

Sponsored Links

Video on Finding the Compound Interest Formula

Math Video Transcript

COMPOUND INTEREST FORMULA

PART 1

00:00:04.070
In this lesson, we will learn about the compound interest formula.

00:00:09.140
Consider a loan of $1000, with the compound interest rate of 10%, and the duration of the loan is 3 years.

00:00:18.000
Calculate the total amount of money that we need to pay back, after 3 years.

00:00:24.070
Before we learn about the compound interest formula, let's see how compound interest works.

00:00:31.030
Let's represent this green bar with the loan amount, $1000.

00:00:36.210
Now, after the first year, the interest will be 10% of the loan amount, $1000.

00:00:44.090
To calculate the interest, I, we multiply $1000, with the interest rate, 10%.

00:00:53.040
Now, before we can calculate, we need to change 10% to a decimal.

00:00:59.110
We can do so, by dividing 10% with 100. This gives 0.1.

00:01:07.240
$1000 multiply with 0.1, gives $100.

00:01:14.070
This is the amount of interest, after the first year.

00:01:18.160
Hence, we can find the amount of money that we owe after the first year, by adding $1000, with $100.

00:01:29.010
This gives $1100. Let's write this down here.

00:01:37.220
After the 2nd year, since the interest is compounding, the interest will be 10% of the current amount, $1100.

00:01:48.030
To calculate the interest, I, we multiply $1100 with 10%.  

00:01:55.170
As calculated earlier, 10% converted to decimal is 0.1.  $1100 multiply with 0.1, gives $110.

00:02:10.010
This is the loan's interest after the second year.

00:02:14.110
With this, we can find the amount of money that we owe after the 2nd year, by adding $1100, with $110. This gives $1210. Let's write this down here.

00:02:33.080
After the 3rd year, since the interest is compounding, the interest will be 10% of the current amount, $1210.

00:02:43.120
To calculate the interest, I, we multiply $1210, with 10%.

00:02:51.190
10% converted to a decimal is, 0.1. $1210 multiply with 0.1, gives $121.

00:03:05.200
Therefore, the interest is $121, after the 3rd year.

00:03:12.040
With this, we can find the total amount of money to pay back after 3 years, by adding $1210, with $121.

00:03:23.080
This gives, $1331. Let’s write it down here.

00:03:31.100
Hence, for a loan with compound interest, the total amount of money that we need to pay back after 3 years is, $1331.

00:03:43.220
In the second part, we will see how we can find the compound interest formula.


PART 2

00:00:04.000
After understanding how compound interest works, let's find the compound interest formula.

00:00:11.040
Consider a loan of P dollars, with the compound interest rate of r%, and the loan duration is 3 years.

00:00:19.080
Find the total amount of money that we need to pay back, after 3 years.

00:00:25.110
Let's start by representing this green bar, with the loan amount, P.

00:00:31.230
Now, after the first year, the loan's interest will be r%, of P.

00:00:38.130
Hence, we can find the interest, I, by multiplying P, with r.

00:00:45.100
With this, we can find the amount of money that we owe, by adding P, with Pr.

00:00:53.040
This gives, P + Pr.

00:00:57.100
Notice that, these two terms have 'P' as a common factor.

00:01:03.100
Hence, we can factorize these 2 terms, by taking out 'P'.

00:01:09.200
By doing so, we have P(1+r).

00:01:15.110
So, this is the amount of money that we owe, after the first year.

00:01:21.180
Next, let's find out the interest at the end of 2nd year.  

00:01:27.150
Before doing so, we let Q = P(1+r). Hence, this expression becomes Q.

00:01:39.180
Since this is a compound interest, the interest will be r%, of Q.

00:01:46.230
Hence, we can find the interest, I, by multiplying Q, with r.

00:01:53.240
Now, we can find the amount of money that we owe, by adding Q, with Qr.

00:02:01.060
By doing so, we have Q + Qr.

00:02:06.050
Again, notice that these 2 terms have 'Q' as a common factor.

00:02:12.050
Therefore, we can factorize these terms by taking out Q. This gives Q(1+r).

00:02:21.090
Let's change Q back to P(1+r). By doing so, we have P(1+r)(1+r).

00:02:34.100
Here, P(1+r)(1+r), gives (1+r)^2.

00:02:43.050
So, after the second year, the amount of money that we owe is, P(1+r)^2.

00:02:51.020
Here, we can see something interesting.

00:02:55.080
We know that, P(1+r) is the same as, P(1+r)^1.

00:03:04.140
Observe that, after the first year, we have P(1+r)^1. After the second year, we have P(1+r)^2.

00:03:20.050
From this, we can guess that, after the 3rd year, the amount money that we need to pay back is, P(1+r)^3.

00:03:31.120
Please verify this, to convince yourself.

00:03:35.180
Hence, if the loan duration is n year, we will have, P(1+r)^n.

00:03:45.090
Therefore, the total amount of money that we need to pay back after n years, A = P(1+r)^n.

00:03:56.000
This is the compound interest formula.

00:04:00.030
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on compound interest formula or pick your choice of question below.

Question 1 on calculating the compound interest
Question 2 on using the compound interest formula

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons