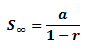Basic Algebra Formulas
Introduction
This page contains basic algebra formulas that
are most
commonly used.
These formulas
are categorized
below:
Sponsored Links
Difference of squares
Difference of cubes
Sum of cubes
Formula for (a+b)2 and (a-b)2
Formula for (a+b)3 and (a-b)3
Formula
Consider this quadratic equation:
Where a, b and c are the leading coefficients.
The roots for this quadratic equation will be:
Where a, b and c are the leading coefficients.
The roots for this quadratic equation will be:
Arithmetic progression
Consider the following arithmetic progression:
Where:
Where:
- a is the initial term
- d is the common difference
The nth term
The nth term, Tn of the arithmetic progression is:
Sum of the first n term
The sum of the first n terms of the arithmetic progression is:
![Sum of the first n term, Sn = n/2[2a + (n-1)d]](http://www.mathexpression.com/image-files/sum-arithmetic.png)
Geometric progression
Consider the following geometric progression:
Where:
Where:
- a is the scale factor
- r is the common ratio
The nth term
The nth term, Tn of the geometric progression is:
The sum of the first n terms
The sum of the first n terms, Sn is:
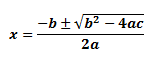
![sum of the first n term, Sn = [a(1-r^n)]/[1-r]](http://www.mathexpression.com/image-files/sum-geometric.png)
The sum to infinity
If -1 < r < 1, the sum to
infinity, S∞ is:
Return to Home Page from
Basic Algebra Formulas
