Equivalent Fractions
Lesson Objective
In this lesson, we will learn the important ideas behind equivalent fractions and how to find these fractions.
About This Lesson
One of the most important thing that we need to know when learning fractions is to be able to find fractions that are equivalent.
A good understanding in this will help you to solve problems that involve fractions with different denominators.
You can proceed by reading the study tips first or watch the math video. You can try out the practice questions after that.

Study Tips
Tip #1
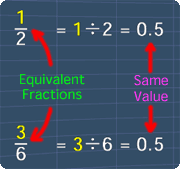
Two fractions are considered equivalent when they have the same value. See the picture below:
Tip #2
Now, we can find equivalent fractions using the following steps:
- Multiply/divide the numerator with a number
- Multiply/divide the denominator with the same number
Below are some examples to illustrate this:

Using Multiplication

Using Division
The math video below will explain more.
Math Video
Lesson Video
Sponsored Links

Please support us by downloading our Fraction Basics app and subscribe to get all 12 video lessons and All Access pass to 8 Zapzapmath Home apps with 180 math games from as low as US$1.67/month:
Apple App Store (iOS) |
Google Play (Android)
Math Video Transcript
00:00:02.100
In this lesson, we will learn about equivalent fraction. We will also learn how to find them.
00:00:09.010
Let's start. Equivalent fractions are fractions that have the same value. What does this means? Let's find out.
00:00:18.040
Consider this fraction, 1/2. We know that this fraction is the same as 1 divides 2, which is equals to 0.5.
00:00:28.150
Again, let's consider this fraction 3/6. This fraction is the same as 3 divides 6, which is also equals to 0.5.
00:00:39.140
Notice that, these 2 numbers are the same.
00:00:44.030
So, this means that these 2 fractions are equivalent.
00:00:49.130
Now, with this in mind, let's examine this visually to understand this better.
00:00:56.230
We are going to use these 2 fractions, 3/4, to further elaborate on this.
00:01:04.140
Let's start finding fractions that are equivalent to 3/4.
00:01:09.120
To find these fraction, we just need to multiply the fraction's numerator, and denominator with the same number.
00:01:17.210
For example, we can multiply the numerator 3, with 2, and the denominator 4, with 2.
00:01:24.230
This gives the fraction 6/8. Now, we can visually see that 6/8, is equivalent to 3/4, because the total height of the colored parts remains the same.
00:01:40.000
Next, let's multiply the numerator 6, with 3, and the denominator 8, with 3.
00:01:47.160
Now, this fraction becomes, 18/24. Again, since the total height of the colored parts are the same, these 2 fractions are equivalent.
00:02:01.070
Now, why do we need to multiply both the numerator and denominator with the same number?
00:02:08.030
In order to explain this, lets say that we only multiply the denominator with 2. This gives 3/8.
00:02:17.050
Here, we can easily see that these 2 fractions are not equivalent. This is because the total height of the colored parts are not the same.
00:02:27.210
Hence, to make them the same again, we need to multiply the numerator with the same number, which is 2 for this case.
00:02:36.090
This gives 6/8, and now these fractions are equivalent again. With this, we can say that equivalent fractions can only be obtained by multiplying the numerator and denominator with the same number.
00:02:51.130
Next, can we also get E.F from division?
00:02:56.110
Let's find out, using this fraction 18/24. Notice that, we can divide the numerator with 6, and denominator with 6.
00:03:08.170
By doing so, we have the fraction, 3/4. Since the total height of the colored parts remains the same, these 2 fractions are equivalent.
00:03:20.230
Here, note that this fraction is a simplified fraction. This is because we are not able to continue to do any more division on it.
00:03:30.080
Now, how about addition or subtraction?
00:03:35.120
Let's find out, by adding 2 to the numerator and denominator. After doing so, we can see that the total heights of the colored parts are not the same.
00:03:48.070
So, addition does not gives E.F.
00:03:55.220
Next, by subtracting the numerator and denominator with 2, again we can see that the total heights of the colored parts are not the same. So, subtraction does not gives E.F.
00:04:10.080
Therefore, we know that, we can get equivalent fractions from multiplication or division, and not from addition or subtraction.
00:04:18.090
That is all for this lesson. Try out the practice question to test your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on equivalent fractions or pick your choice of question below.
- Question 1 on finding fractions that are equivalent.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


