Exponent Laws - Part 1
Lesson Objective
This lesson shows you the basics behind the first three exponent laws. You will also see how these laws are derived...
About This Lesson
Let's say that you need to find out the result (in the form of 2???) of the following multiplication:
Now, if you try to solve it by calculating the actual value of 21000 or 21007, you will soon realize that it is very difficult to do so.
Fortunately, with the help of the first exponent law, you will quickly know that:
21000 x 21007 = 21000 + 1007
= 22007
This lesson shows you the basics behind the first three exponent laws. It is good to understand these laws first before using them.

Study Tips
Tip #1
When you are given a term with a form of am, it is defined that:
a is the base
m is the exponent
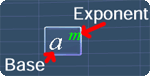
For example, consider the term 25, referring to the definition above:
2 is the base
5 is the exponent
Tip #2
It is very important to understand how the exponents laws are formulated. Once you fully understood them, it's easier to avoid mistakes when applying these laws.
For example, usually those who don't understand the logic behind these laws will tend to make this mistake:
23 x 22 = 23 x 2 (wrong application of the first law)
= 26
= 64 (oops!!...mistake)
When you use your calculator to check, you will find out that actually:
23 x 22 = 8 x 4
= 32 (correct!)
So, do realize the consequences for applying the exponent laws without understanding them.
Now, watch the following math video to know more.
Math Video
Click play to watch
Sponsored Links
Math Video Transcript
Exponent Laws Lesson
00:00:01.010
This lesson shows you the basics of the law of exponents.
00:00:06.040
It is very important to understand the logic behind these laws before you use them.
00:00:11.210
Now, let us start with the first law.
00:00:15.100
For us to understand the first law, let's consider multiplying 2 power of 3 with 2 power of five.
00:00:22.160
Now, we can also write two power of 3 as, 2 multiply by 2, multiply by 2.
00:00:29.170
Similarly, 2 power of 5 is equals to 2 multiply by 2, multiply by 2, multiply by 2, multiply by 2.
00:00:39.080
With this, we can see that we are multiplying eight twos.
00:00:44.010
Therefore, we get 2 power of 8.
00:00:47.180
Now, notice this, we can also get 8, by just adding 3 and 5 together.
00:00:54.230
So, 2 to the power of 8 is also equals to 2 to the power of 3 plus 5.
00:01:01.050
With this observation, we can now formulate the first law.
00:01:06.220
Let's first replace these numbers to alphabetical letters. This gives 'a' to the power of 'm' multiply by 'a' to the power of 'n'.
00:01:16.210
By referring to this, we can deduce that by multiplying 'a' to the power m with a to the power of 'n', we get 2 to the power of 'm' plus 'n'.
00:01:31.120
Finally, here we have, the first exponent law.
00:01:34.230
Let's take a look at the 2nd law of exponent. For us to understand the second law, let us consider dividing 2 to the power of 5 with 2 to the power of 3.
00:01:45.200
Now, two to the power of 5 is equals to 2 multiply by 2, multiply by 2, multiply by 2, multiply by 2.
00:01:55.070
Similarly, 2 to the power of 3 is equals to 2 multiply by 2, multiply by 2.
00:02:02.210
Now, both of the twos here cancel off each other. Same goes for here, and here.
00:02:11.010
What we have now is 2 multiply by 2, which is equals to 2 power of 2.
00:02:17.040
Now, notice this, we can also get the exponent, 2, by minus off 5 with 3.
00:02:25.010
So, 2 to the power of 2 is also equals to, 2 to the power of 5 minus 3.
00:02:32.070
With this observation, we can now formulate the second law.
00:02:37.140
Let's first replace these numbers with alphabetical letters. This gives 'a' to the power of 'm' divides by 'a' to the power of 'n'.
00:02:47.070
By referring to this, we can deduce that by dividing 'a' to the power of m with 'a' to the power of 'n', we get, 'a' to the power of 'm' minus 'n'.
00:03:00.040
Finally, here we have, the second exponent law.
00:03:07.000
Let's take a look at the third law of exponent. For us to understand the third law, let us consider bracket 2 the power of 3 to the power of 4.
00:03:18.090
We can see that this term is equals to, 2 to the power of 3, multiply by 2 to the power of 3, multiply by 2 to the power of 3, and multiply by 2 the power of 3.
00:03:32.070
By applying the first law, we get 2 to the power of 3 plus 3 plus 3 plus 3.
00:03:39.210
This is equals to, 2 to the power of 12.
00:03:43.180
Now, notice this, we can get the exponent, 12 by just multiplying 3 with 4.
00:03:51.120
Therefore, we can write this term as, 2 to the power of 3 multiply by 4.
00:03:58.060
With this observation, we can now formulate the 3rd law.
00:04:02.150
Let's first replace these numbers with alphabetical letters. We get bracket, 'a' to the power of 'm', to the power of 'n'.
00:04:12.220
By referring to this, we can deduce that, 'a' to the power of 'm', to the power of 'n', is equals to 'a' to the power of 'm' multiply by 'n'.
00:04:24.160
Finally, here we have, the third exponent law.
00:04:29.240
That is all for this lesson. The next lesson will show you how to formulate the rest of the exponents laws.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on exponent laws or pick your choice of question below.
- Question 1 on the basics of the first three exponent laws
More Lessons
Here are more lessons that you might be interested:
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


