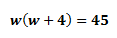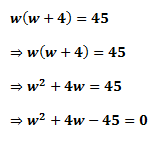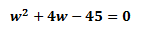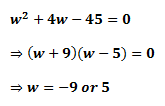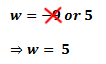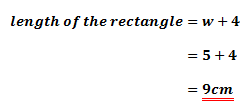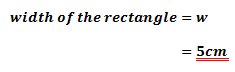Find the dimensions of a rectangle

by a visitor

Question

The area of a rectangle is 45 square cm. If the length is 4 cm greater than the width, what is the dimensions of the rectangle?

Answer

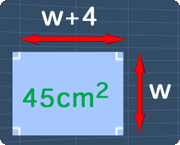
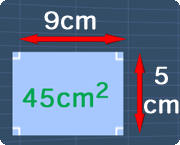
The picture below shows the rectangle with the area of 45cm². Now, let the width be w. Since, the length is 4cm greater than the width, the length will be w+4 cm. 


Before we can find the dimensions of the rectangle, we need find w first. Here's how:

1) Write an equation that relates 45cm², w+4 and w.
To do so, we know that the area of the rectangle, 45cm² can be found by multiplying w with  w+4. Hence, we have: 
To continue, we need to remove the bracket and simplify the equation. This is shown below:  

2) Solve the Quadratic Equation
Notice that, now we have a quadratic equation:
 
To find w, we need to solve the quadratic equation. One way to do so is to factorize the quadratic equation. Hence, we have:
Now, since w is the width of a rectangle. There is no way it can be a negative number. Therefore, w must be 5. With w = 5. The...
...and the... Below is the rectangle with its dimensions: