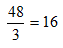Problem Solving: Find the age of the daughter

by Abdul

Question

If the age of a father is 2 times greater than his son and 3 times than his daughter, and their total age is 88. What is the age of daughter?

Answer

STEP 1:    You are asked to find the age of the daughter. If you assume a variable for the daughter’s age, you will not be able to proceed any further with the calculations because no adequate information has been provided.

Choose a variable to represent the age of the father, say, f. Since the relation the age of father has with the age of his son and daughter, and the total age are known, you can frame an equation.

STEP 2:    The age of the father is two times that of his son. This implies that the son’s age is ^f/₂ . Using the relation between the age of father and the age of daughter, you get her age as ^f/₃.

The three ages add up to 88.Now we have an equation in terms of one variable that we can solve.

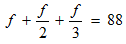
STEP 3:   You see that the denominators of the fractions on the left are not the same. To be able to perform the addition, we need fractions with like denominators (equivalent fractions). If we multiply the first fraction by ⁶/₆, the second by ³/₃, and the third by ²/₂ , we can get equivalent fractions.
Now, simply add the numerators of the fractions writing the denominator only once.
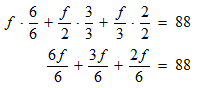
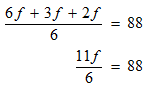
STEP 4:    Isolate the variable.
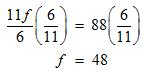
The age of the father is 48 years. But, you are asked to find the daughter’s age. Divide 48 by 3 for this purpose.The age of the daughter is 16 years.