Scalene Triangle
Lesson Objective
In this lesson, we will learn about scalene triangles...
About This Lesson
In this lesson, we will:
- learn what are scalene triangles.
- see some examples on identifying them.
The study tips below will give you a short summary on this.
The math video below will explain in depth about this. Furthermore, it will show some examples so that you can understand this lesson better.
Study Tips
Tip #1
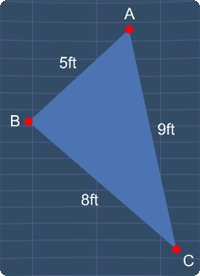
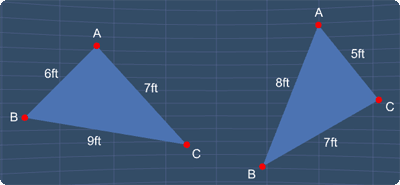
When a triangle has three sides (edges) of different lengths, this triangle can be called a scalene triangle. See some examples below:
Tip #2
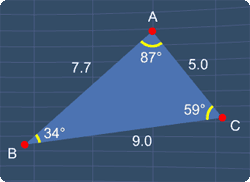
Since this type of triangle has three sides of different lengths, all of its internal angles will be different as well. See the picture below:
The math video below will explain more...
Math Video
Lesson Video
Sponsored Links
Scalene Triangles from MathExpression.com on Vimeo.

Interact and have fun learning of the types of triangles by downloading our Zapzapmath Home Grade 4 app and playing Shape Detective:
Apple App Store (iOS) |
Google Play (Android)
| |
Math Video Transcript
00:00:03.150
In this lesson, we will learn about scalene triangle (ST).
00:00:09.020
A triangle is a ST, when all the sides of the triangle, have different lengths..
00:00:16.100
Now, to demonstrate this, let's move vertex 'C' to the left.
00:00:22.230
Here, we can see that, all the 3 sides of this triangle have different lengths. Hence, this is a ST.
00:00:33.190
It is important to note that, the interior angles will also be different.
00:00:40.000
Let's continue to move point ‘C’.
00:00:43.210
Now, when these two sides have the same length, it is not a ST.
00:00:50.220
As we continue to move 'C', we will get a right triangle.
00:00:56.030
A right triangle, can also be a ST, when the length of each side is different.
00:01:04.000
However, it will not be a scalene, if two of its sides, have the same length.
00:01:12.030
Let's see some examples.
00:01:15.100
Is this a ST?
00:01:19.150
Since this triangle has 3 sides of different lengths, this is a ST.
00:01:26.180
Next example. How about this triangle?
00:01:32.140
We can see that, these angles are not the same.
00:01:37.080
This means that, these 3 sides must have different lengths.
00:01:43.040
Hence, this is a ST.
00:01:47.130
Last example. Now, these 2 sides have the same length.
00:01:55.190
Therefore, this is not a ST.
00:02:00.140
That is all for this lesson.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on scalene triangles or pick your choice of question below.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


