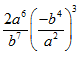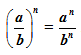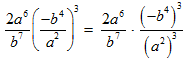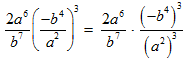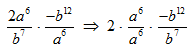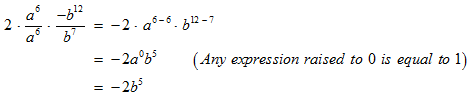Simplify the Expression (2a^6/b^7)(-b^4/a^2)^3

Question

Simplify the expression (2a^6/b^7)(-b^4/a^2)^3

Answer

STEP 1:   Observe the given expression:If you observe the expression, then you notice that it contains a term in which a quotient is raised to a power. The first step in simplifying the expression will obviously be to simplify that term.

The exponent law which can be helpful for this purpose is:The law simply means to bring the power into each term of the quotient. See what happens when we apply the law.STEP 2:    The numerator and the denominator of that fraction still contain powers raised to the third power. Multiply the exponents making use of the law:
                                        (a^m)ⁿ = a^mn

We get:STEP 3:     What we want to do here is to write as a product such that all expressions with like bases are brought together.STEP 4:     Now, the operation left is to divide powers with like bases. When you divide, the exponents subtract.
 
The final simplified expression that you get is –2b⁵.