
Simplifying an expression by removing the brackets
by Kristina
(USA)
Question
I am trying to remember what the purpose is for the brackets in an equation. Example: 5{4(y – 4) + 15 – 2(5y – 3) +1}. Can someone please explainAnswer
STEP 1: You are given an algebraic expression that contains parentheses (), brackets [], and curly braces {}. All these are grouping symbols that are used to make you perform the operations within them ahead of other operations. Removing the innermost grouping symbols is the first step to be done in simplifying the expression.Consider 4(y – 4). The factor 4 is distributed over the difference y–4. To remove the parentheses in this term, first multiply 4 by y. You get 4y. Multiply 4 by –4 next. You get –16. So, the result that you get is 4x – 16.
STEP 2: Now, you can follow the same method to remove the parentheses in 2(5y – 3). This gives 2(5y – 3) = 10y – 6.
Put the new expressions back into the original expression.
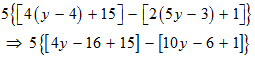
STEP 3: Now, the expression contains only brackets and curly braces. The next move from your side should be perform all the operations possible within the two sets of brackets.
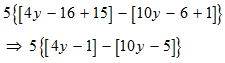
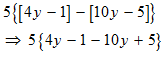
STEP 5: Now, the expression contains only curly braces. Perform all operations possible within them first.
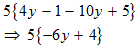
STEP 6: Apply the distributive law to open the curly braces.
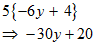
Comments for Simplifying an expression by removing the brackets
|
||
|
||
|
||
|
||
|
||
|
||


