Slope-Intercept Form of a Line
Lesson Objective
In this lesson, we will examine the slope-intercept form of the equation of a line.
About This Lesson
After learning about the slope, x-intercept and y-intercept of a line, it is time for you to learn about the equation of a line that has both the slope and y-intercept (slope-intercept form of a line).
This lesson will show you how the graph of the line will change for different values of slope and y-intercept.
You should proceed by reading the study tips and watch the math video below. After that, you can try out the practice questions.
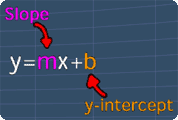
Study Tips
Tip #1
This lesson involves the slope and y-intercept. If you need to recall them, you can watch the math videos in:
Tip #2
An equation of a line can be written in many forms. Some of these forms are listed below:
- Slope-Intercept Form
- Point-Slope Form
- Two Point Form
An equation of a line can be changed into any of these forms.
Now, watch the following math video to learn more.
Math Video
Click play to watch video
Sponsored Links
| |

You can contribute to the development of this site and keep it free by getting all six video lessons and volume of solids and calculator app for just US$1.99 from Apple App Store.
I'd like to contribute or to know more about the appMath Video Transcript
00:00:01.190
In this lesson, we will examine the slope-intercept form of an equation of a line.
00:00:07.080
The equation of a straight line can be written in the form of y =, m x + b, where m is the slope, and b is the y-intercept.
00:00:16.220
As for y and x, they are just variables, and can be represented in the graph as y-axis and x-axis respectively.
00:00:25.100
As you can guess, this equation of a line is in the Slope-Intercept form because it contains both the slope and y-intercept.
00:00:32.190
Now, to understand more about y = m x + b, let's take a look at this line: y = 2x + 3.
00:00:42.200
By comparing y = 2x +3 with y = m x +b, we can see that the slope of the line is 2, and the y-intercept is +3.
00:00:53.170
Now, the line for this equation, y = 2x+3 is shown on the graph.
00:01:00.200
Since the y-intercept is +3, naturally, this line will cross the y axis at 3.
00:01:08.160
Alright, when I decrease the y-intercept, notice how the line changes accordingly.
00:01:14.220
When the y-intercept is changed to +2, note that the line will cross the y-axis at +2.
00:01:22.130
We will observe a similar behavior when the y-intercept is changed to positive 1, zero, -1, -2, and so on.
00:01:34.090
Also, notice that, since we are only changing the y-intercept, the slope of the line remains the same.
00:01:47.100
Next, let's examine the slope, m. When I change the slope, notice how the steepness of the line changes.
00:01:55.200
As I increases the slope from +2 to +3, we can see that the line becomes steeper.
00:02:03.160
So, you can see that, the line becomes steeper as the slope continues to increase.
00:02:09.240
Also, note that, when the slope is positive, the line slants upward to the right.
00:02:16.170
Next, since we only change the slope, the y-intercept remains same and the line will naturally crosses the y-axis at +1.
00:02:26.080
Alright, what happens to the line when the slope, m, is zero or negative?
00:02:33.020
To know this, let us decrease the slope.
00:02:35.240
Now, see that when the slope is zero, the line becomes parallel to the x-axis.
00:02:43.170
As the slope becomes negative, the line now slants upward towards the left, and the steepness of the line increases as the slope becomes more negative.
00:02:54.020
That is all we need to know about y = mx + b for now, we will learn more about in the next lesson.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on slope-intercept form or pick your choice of question below.
- Question 1 on the basics of slope-intercept form
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


