Adjacent Angles
Lesson Objective
In this lesson, we will learn about adjacent angles.
About This Lesson
In this lesson, we will:
- What are adjacent angles.
- See some examples on identifying them.
The study tips below will give you a short summary on this.
The math video below will explain in depth about this. Furthermore, it will show some examples so that you can understand this lesson better.
Study Tips
Tip #1
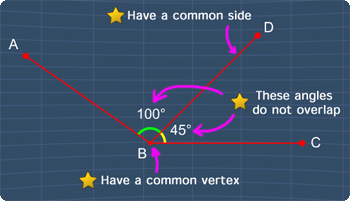
There are three conditions that must be met when identifying whether two angles are adjacent angles. These conditions are:
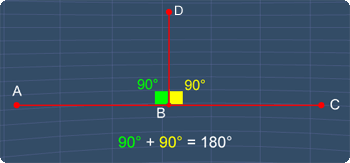
Tip #2 - Special Case: Supplementary Angles
When two angles are adjacent and these angles add to 180°, these angles become supplementary angles.
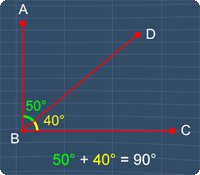
Tip #3 - Special Case: Complementary Angles
Now, if two angles are adjacent and these angles add to 90°, these angles become complementary angles.
The math video below will explain more...
Math Video
Math Video Transcript
00:00:04.090
In this lesson, we will learn about adj. angles.
00:00:09.120
Let's take a look at these two angles. 45 degrees and 110 degrees respectively.
00:00:18.020
Now, these two angles are adjacent angles.
00:00:23.180
This is because, these 2 angles shares a common side, BD, a common vertex B and these 2 angles do not overlap.
00:00:37.230
Next, when I move this arm BD, take note of the adj. angles.
00:00:52.060
Let's see some examples.
00:00:55.200
Are these adj. angles?
00:00:59.020
Let's find out. We can see that, these 2 angles have a common side AC and a common vertex A.
00:01:09.020
Furthermore, these 2 angles do not overlap. Therefore, these are adj. angles.
00:01:19.110
Next example, how about these 2 angles?
00:01:26.110
Here, we can see that, these angles have a common vertex A and common side AB. However, these angles overlap.
00:01:39.080
Hence, these are not adj angles.
00:01:44.150
Next, are these adj. angles?
00:01:50.120
Here, these 2 angles share the same vertex A.
00:01:55.070
However, these angles do not have a common side.
00:02:00.150
Hence, these are not adj. angles.
00:02:05.060
Final example, these 2 angles have a common side BC but, do not have a common vertex.
00:02:16:010
Hence, these are not adj. angles.
00:02:20.230
That is all for this lesson.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on adjacent angles or pick your choice of question below.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


