
Algebra Story Problem: Find the speed of the current
Question
Two miles upstream from his starting point, a canoeist passed a log floating in the river's current. After paddling upstream for one more hour, he paddled back and reached his starting point just as the log arrived. Find the speed of the current.Answer
STEP 1: You are asked to find the speed of the current. Assume a variable for this quantity, say, c. We come across some other quantities in the given information which can also be denoted by variables for ease in reference.See how the parentheses get cleared when each term inside the parentheses is multiplied by the factor outside.
- t – total time, right from when the canoeist sees the log till he reaches back at the starting point.
- r – rate of the canoeist
- x – distance paddled upstream by the canoeist after he sees the log.
This will help you to frame an equation, 2 = ct. You can also rewrite it as t = 2/c.
STEP 3: It is to be noted that t is the total time taken by the canoeist to travel the upstream distance x, then downstream and finally 2 miles.
Since the direction of current is against that of the canoeist, the time taken to cover his upstream journey will be:
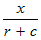
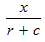
Also, the time it takes for the canoeist to cover the final 2 miles downstream is:
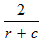
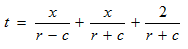
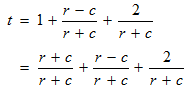
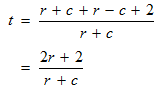
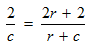
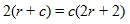
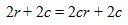
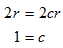
Comments for Algebra Story Problem: Find the speed of the current
|
||
|
||
|
||
|
||


