Determine the number of real-number solutions

Question

Determine the number of real-number solutions to the equation from the given graph 4x² + 1 = 4x, given the graph of y = 4x -4x² -1.

Answer

STEP 1:   We note that both the given equations are in the variable x, and are of the quadratic form ax² + bx + c. Recall the fact that the solutions of an equation of the form ax² + bx +c = 0 are its x-intercepts.

The solutions of such equations can be easily found out by sketching the respective graphs. To be clearer we graph each of the given equation, and then identify the points where the graph intersects the x-axis.

We shall first sketch the graph of 4x² + 1 = 4x. Here, the point to be noticed is that to plot the equation we rewrite it in the form
y = 4x² – 4x + 1.

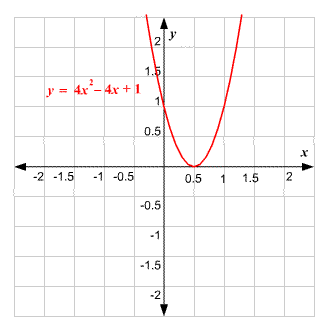
STEP 2:    We have already discussed the fact that the solution of the equation is the x-value at which the respective graph intersects the x-axis. From the graph, it is clear that it intersects the x-axis at
x=0.5.

STEP 3:    The equation we have to graph now is y = 4x² – 4x + 1. We plot the graph similar to what we have done before.
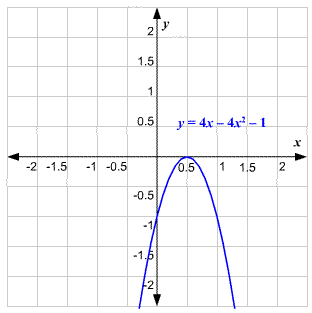
Again, it is found that the graph intersects the x-axis at the same point x = 0.5. So, here also the solution to the equation is x = 0.5.

There is only one real number solution to both the equations.