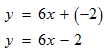Effects of changing the slope and the y-intercept

Question

Using y = 3x + 1, find the equation of a second line by multiplying the slope by 2 and shifting the line down by 3 units.

Answer

STEP 1: You are given the equation of a line to be used it to find the equation of another line which has double the slope and is vertically shifted downwards.

Start working by finding the slope of the given line. Since the equation is already in the slope-intercept form (y = mx + b), you can easily find the slope.

Make a note of what each variable in the equation stands for:

Compare with the standard form.

The slope of the given line is 3. But, the new line has double the slope.

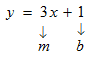
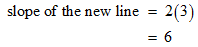
STEP 2: You also have the value of the y-intercept from the comparison as 1. The corresponding point is (0, 1). Now, if the line gets shifted downwards by 3 units, there will also be a change in its y-coordinate. It gets reduced by 3 units.

The new coordinate point is (0, –2), and hence the new y-intercept is –2.

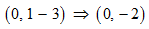
STEP 3: Now, the only step left is to substitute for m and b in the slope-intercept form.