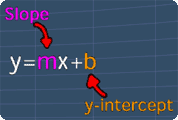Math Expression: Equation of Line Practice

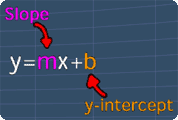
Given the points (3,-3) and (-3, 1). Determine the equation of the line that passes through these points.

You can use the picture shown on the right as reference.

Step 1

First, to determine the equation of the line, we should start with the Slope-Intercept Form of an equation of a line.

From the picture, we only need to find the values of the slope(m) and y-intercept(b).

After finding them, we just replace m and b with these values. That's it.
Step 2

Now, with the given 2 points (3,-3) and (-3,1), we can use them to find m using the Slope Formula as shown on the right.

To use this formula, we need label these points as Point 1 and Point 2. Let's label (3,-3) as Point 1 and (-3,1) as Point 2.

By doing this, we have:
Step 3

Now, we substitute these values into the slope formula.

Hence, the we get the slope, m = -2/3
Step 4

With m = -2/3, the equation becomes:

Next, we have to find b. To do so, we can pick a point on the line and substitute its x- and y-coordinates into the equation above.
Step 5

We can just pick any of the given points, (3,-3) or (-3, 1). Let's pick the point (-3, 1) where:

x = -3 and y = 1

Substituting x and y into the equation, we get:

Now, let's solve for b:

With this, we have the y-intercept, b as -1
Step 6

With b = -1, the equation becomes:

From the equation of the line above, clearly the answer is C.