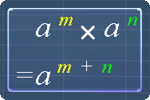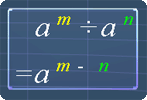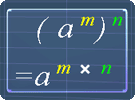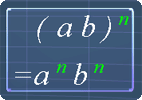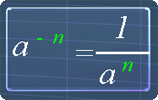Exponent Law Practice Question
Question 1
Which of the following equations are true?
- (ab)0 = 1
- (a2b)3 = a5b2
- (a10b-3)0 = z0
The following pictures are the exponent laws. You can use them as reference.
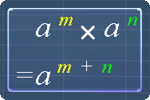
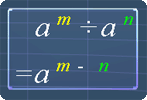
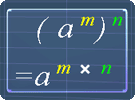
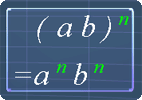

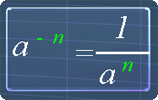
Which of the following equations are true?
The following pictures are the exponent laws. You can use them as reference.