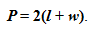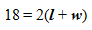Find the length and width of a rectangle

Question

Draw a rectangle that has a perimeter of 18 cm and an area greater than 18 sq.cm. What are the dimensions?

Answer

STEP 1:    It will be helpful if you can recall the basic properties of a rectangle. A rectangle is defined by the dimensions length and width. It has four sides, and also the opposite sides of a rectangle have the same length.

You are given the perimeter of a rectangle. The perimeter, as you know, is the total distance along the outside of the rectangle. The formula used to calculate perimeter is:In the formula, the variables l and w denote the length and width of the rectangle, respectively.

STEP 2:    Since you know the value of the perimeter, you can make the replacement in the formula.By dividing both the sides by 2, the equation changes to
9 = l + w, or l + w = 9.

STEP 3:    Think of the possible dimensions the rectangle can have if the sum of the length and width equals 9 cm. But, it is given that area of the rectangle has to be greater than 18 sq. cm. This means that the product of the length and width must be greater than 18.

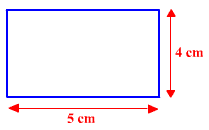
Try different values for l and w such that the sum equals 9. Find the corresponding products, and then make a table of values.If you observe the table, then you can find that the area of the rectangle is greater than 18 only when the dimension of the rectangle is either 4 cm by 5 cm, or 5 cm by 4 cm.

STEP 4:    Choose any of the two desirable dimensions. Then, finally draw the rectangle.