Find the x-intercept and y-intercept

by Julee
(USA)

Question

Find the x- and y- intercepts of the line using these coordinates, (–2, –5) and (6, 1).

Answer

STEP 1:    Before getting started, it will be helpful if you could recollect the basic definition of the intercepts. By the x-intercepts, we mean the x-coordinate of a point where a graph crosses the x-axis. Similarly, y-intercept refers to the y-coordinate of a point where a graph crosses the y-axis.

To find the intercepts, we either need the graph or the equation defining the graph. Since we are given only two coordinate points, you will need to frame the equation using these points and then find the intercepts.

STEP 2:    You can use the slope-intercept form to find the equation of the line. By the slope-intercept form, we refer to an equation of the form:
                                        y = mx + b

Make a note of what each variable in the equation stands for:
Since the value of m is unknown, the first step is to calculate the slope of the line.

STEP 3:   If (x1, y1) and (x2, y2) are two coordinate points through which a line passes, then the slope of the line defined by these points is:
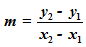
Choose (x1, y1) = (–2, –5) and (x2, y2) = (6, 1).

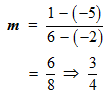
By substituting the value obtained in the slope-intercept form, you get the equation:
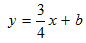
STEP 4:    The value of b is still unknown. Since the line is said to pass through (–2, –5) and (6, 1), select either of the points and substitute the respective values for x and y. We shall select the point (6, 1).
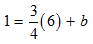
STEP 5:    Now, solve the equation for b.

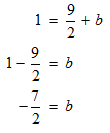
With the values obtained for m and b, the equation of the line takes the form:

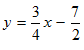
STEP 6:    Now, you can easily find the intercepts. By referring to the definition, we understand that the y-intercept is some coordinate point like (0, y), and the
x-intercept is (x, 0).

Since the x-coordinate is 0 for y-intercept, substitute the 0 for x in the equation.Similarly, find the x-intercept by replacing y with 0.
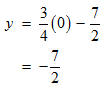
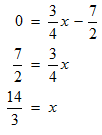
You finally get the x-intercept as (¹⁴/₃,0),and the y-intercept as (0,-⁷/₂).