Multiplying Fractions

Lesson Objective

In this lesson, we will learn the basics behind multiplying fractions and will be using some examples to explain how this multiplication works.

Study Tips

Tip #1

When multiplying fractions, the denominators don't have to be the same.

Tip #2 - How to Multiply Fractions

Below are steps to multiply two fractions:

Multiply the numerators:
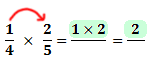
Multiply the denominators:
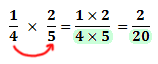
Simplify the fraction if possible:
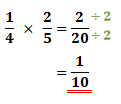
$Simplify the fraction 2/20$

Tip #3 - Multiplying Mixed Fractions

The example below shows how we can multiply two mixed fractions:

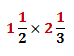
Convert the mixed fractions to improper fractions:
$Convert mixed fractions to improper fractions$
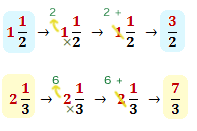
After the conversions, we have:
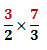
Now, multiply the fractions as usual. Simplify if possible:
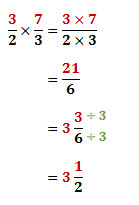
$Multiply the converted fraction, 3/2 with 7/3$

Watch the math video below for more explanation.

Math Video

Lesson Video

Sponsored Links

Math Video Transcript

00:00:02.100
In this lesson, we will learn the basics behind multiplying fractions.

00:00:07.180
Now, compared to adding or subtracting fractions, it is easier to multiply fractions.

00:00:14.130
This is because when we multiply fractions, we don’t have to make the denominators the same.

00:00:21.030
For example, let's multiply, 2/3 with 4/5.

00:00:29.020
To do so, we just need to multiply the numerators together.

00:00:34.190
Therefore, we multiply 2 with 4. This gives 8.

00:00:40.100
Next, we multiply the denominators together.

00:00:44.130
Therefore, we multiply 3 with 5. This gives 15.

00:00:51.020
So finally, we can see that this fraction multiplication gives 8/15.

00:00:57.180
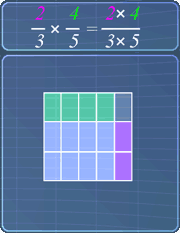
Now, let's visually examine how this multiplying fractions work.

00:01:03.000
We can represent 2/3, with this rectangle. Similarly, we represent 4/5, with this rectangle.

00:01:13.130
When we multiply these fractions, visually, it means that we are combining these rectangles.

00:01:20.210
When the green and purple rectangles overlap, they give blue rectangles.

00:01:26.090
Here, we can see that, these 8 blue rectangles are represented by the numerator 8.

00:01:32.150
Also, notice that there are total of 15 rectangles, which are represented by the denominator 15.

00:01:43.240
Alright, let's take a look at more examples on multiplying fractions.

00:01:50.100
Let's multiply, 7/8, with 2/5.

00:01:57.120
First we multiply the numerators. So, we multiply 7 with 2. This gives 14.

00:02:12.030
Next, multiply the denominators. So, we multiply 8 with 5. This gives 40.

00:02:18.220
Now, we have the fraction, 14/40.

00:02:23.210
Notice that, we can simplify this fraction. To do so, we divide the numerator and denominator with 2.

00:02:32.070
This gives the simplified fraction, 7/20.

00:02:38.120
Next example, let's multiply 1/3, with 3 1/2.

00:02:45.080
Notice the mixed fraction here?

00:02:48.050
It is important to change it to an improper fraction before multiplying.

00:02:53.180
To do so, first, we multiply 2 with 3. This gives 6.

00:03:01.100
Next, we add 6 with 1. This gives 7. This 7 becomes the improper fraction's numerator.

00:03:11.150
Hence, we have the improper fraction, 7/2.

00:03:16.170
We can now multiply these fractions.

00:03:20.230
First, multiply the numerators. So, we multiply 1 with 7. This gives 7.

00:03:31.000
Next, we multiply the denominators. So, we multiply 3 with 2. This gives 6.

00:03:41.230
Notice that, 7/6 is an improper fraction. Now, rather than leaving the answer like this, it is recommended to change it to a mixed fraction, by using long division.

00:03:53.240
Here's how. 7/6 is the same as, 7 divides 6. Now, this division gives the quotient 1. This quotient is actually the whole number for the mixed fraction.

00:04:11.160
Next, we multiply 1 with 6. This gives 6. 7 minus 6 gives the remainder as 1.

00:04:21.230
This remainder, 1, is actually the mixed fraction's numerator.

00:04:29.030
So here, we have the answer in mixed fraction, 1 1/6.

00:04:35.240
That is all for this lesson. Try out the practice question to further your understanding.

--End of Multiplying Fractions Transcript--

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on Multiplying Fractions or pick your choice of question below.

Question 1 on multiplying two proper fractions
Question 2 on multiplying a mixed fraction with a proper fraction

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons