Positive & Negative Slope
Lesson Objective
This lesson shows you under what circumstances a line can have a negative slope, positive slope, zero or infinite slope.
About This Lesson
After you have familiarized with the slope formula. It is time to further analyze the slope of a line.
In this lesson, we will see under what circumstances a line can have:
- Positive Slope
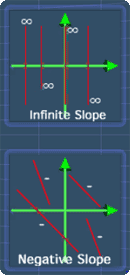
- Negative Slope
- Zero Slope
- Infinite Slope
You can proceed by reading the study tips first or watch the math video. You can try out the practice questions after that.
Study Tips
Tip #1
Understand how the 'change in y' and 'change in x' are calculated. To recall them, you can watch the first math video in the slope of a line lesson.
It is useful to learn about the slope formula so that it will be easier to understand this lesson.
Tip #2
We will come across something called 'infinite slope'. To comprehend it, let me explain 'infinitely large number' first in a simple way.
Observe the following sequence:
2 ÷ 0.1 = 20
2 ÷ 0.001 = 2000
2 ÷ 0.00001 = 200000
2 ÷ 0.0000001 = 20000000
2 ÷ 0.000000001 = 2000000000
2 ÷ 0.00000000001 = 200000000000
2 ÷ 0 = infinitely large number
Notice that when 2 is divided by a smaller number, you will get a larger number. Now, if 2 is divided by 0, we can roughly say that we will get an infinitely large number.
Why roughly? This is because it would be more accurate to say that the number is 'undefined'. But, for the sake of simplicity, I will not explain this for now.
Now, watch the following math video to learn more.
Math Video
Click play to watch video
Sponsored Links
Math Video Transcript
Transcript for Positive and Negative Slope
00:00:01.240
The objective of this lesson is to show you under what circumstances, that the slope of a line is positive or negative.
00:00:09.010
Also, you will get to see in what way the slope becomes zero or infinite.
00:00:14.080
Now, consider this line. Since this line is parallel to the x-axis, the 'change in y' is 0.
00:00:23.100
Now, 0 divides by 4 gives 0.
00:00:27.110
Therefore, this line has the slope of zero.
00:00:30.220
Alright, As I move this point up, notice that the line slants upwards to the right, and the value of the slope increases.
00:00:39.090
Also, notice that the value of the slope is a positive number.
00:00:44.010
This is because the 'change in y' and 'change in x' are positive. Hence, a positive number divides by a positive number gives a positive.
00:00:54.210
Now, as the slope gets higher, this line will eventually becomes parallel to the y-axis.
00:01:01.110
Here, we can see something interesting, the slope is now infinite.
00:01:06.160
This is because of the 'change in x' is zero, and for the case of slope, any non zero number divides by 0 gives infinite.
00:01:15.160
Let's continue, as I move the point to the left, the line slants downwards to the right.
00:01:21.180
Notice that, we now have negative slope.
00:01:25.100
This is because of the 'change in x' is a negative number.
00:01:29.220
So, a positive number, divides by a negative number, gives a negative number.
00:01:36.220
As I move this point down, the slope gradually becomes zero.
00:01:42.180
Now, when I continue to move this point down, the line again slants upwards to the right again.
00:01:50.030
Notice that, the slope becomes positive.
00:01:54.140
As I move this point to the right, the value of the slope becomes higher.
00:01:59.140
Eventually, when the line is parallel to the y axis, the slope becomes infinite.
00:02:06.030
Let's continue to move further to the right, the slope now slants downwards to the right.
00:02:12.090
Notice that, the slope becomes negative.
00:02:16.040
Now, from these observations. we see that the value of the slope can be negative, positive, zero or infinite.
00:02:24.050
Let's examine positive and negative slope further.
00:02:29.050
It seems that when the line is slant upwards to the right, the slope is positive.
00:02:35.140
Further example, this line slants upward to the right and the slope is positive.
00:02:42.130
It is the same here, this line slants upward to the right and the slope is positive.
00:02:48.030
Finally, this line slants upward to the right and the slope is positive.
00:02:54.060
However, when the line slants downwards to the right, the slope is negative.
00:03:00.180
Further example, this line slants downward to the right and the slope is negative.
00:03:06.210
It is the same here, this line slants downward to the right and the slope is also negative.
00:03:15.030
Let's summarize on what we have observed, when we see the line slants upwards to the right, the slope is positive.
00:03:23.180
When the line slants downwards to the right, the slope is negative.
00:03:29.130
To briefly note, when the line is parallel to the x-axis, the slope is 0.
00:03:37.010
When the line is parallel to the y-axis, the slope is infinite.
00:03:43.070
That is all for this lesson, try out the practice question to further your understanding.
End of Transcript for Positive and Negative Slope
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on positive and negative slope or pick your choice of question below.
- Question 1 on positive and negative slope.
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


