Problem Solving: Find the time for the second bus to catch up

by Katie
(USA)

Question

A bus leaves a station at 8:00 a.m. and averages 30 mi/h. Another bus leaves the same station following the same route two hours after the first and averages 50 mi/h. When will the second bus catch up to the first?

Answer

STEP 1:   We are given that the first bus leaves a station at a rate of 30 mi/h at 8.00 am and that the second bus leaves the same station two hours later at a rate of 50mi/h. Assume a variable for the time taken by the first bus to travel, say, t.

STEP 2:    Recall the formula:
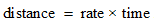
In this case, the distances are the same, so we just need to set the rate × time equal for both the cases.
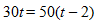
STEP 3:    We can see that 50 is distributed over the difference t – 2. To remove the parentheses in this expression, first multiply 50 by t – 2. To remove the parentheses in this expression, first multiply t. We get 50t. Multiply 50 by -2 next. The result that you get is 30t = 50t – 100.

STEP 4:    Now, we have to isolate the variable terms on one side and the constant terms on the other side.

Subtract 50t from both sides of the obtained expression and simplify.
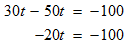
STEP 5:    Isolate the variable t, by dividing both sides of the obtained expression by -20. This is the time of travel for the first bus till the second bus catches up with it.

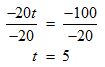
STEP 6:   Now you have to find the time at which the second bus catch up to the first bus. We know that the first bus leaves the station at 8 00 am. So we have to add 5 hrs to the starting time of the first bus:

8.00 am + 5 hours = 1.00 pm

The second bus catches up to the first by 1.00 pm.