
Problem Solving - Find the total time to paint a house
Question
If Sally can paint a house in 4 hours, and John can paint the same house in 6 hours, how long will it take for both of them to paint the house together?Answer
STEP 1: Analyzing the given problem is the first step to be done. You are given the time taken by the two people to paint the house. With these values, the part of work done by each person in an hour can be found. (Recall that the rate of work done is the reciprocal of time taken.)Sally paints the house in 4 hours. So, the part of the work that she completes in 1 hour will be 1/4. Similar is the case with John. He completes 1/6 of the work in an hour.
The total work done by the two people is the sum of the rates.
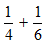
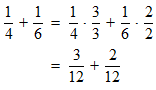
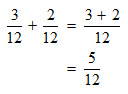
STEP 4: You have the total amount of work done by the two as 5/12. But, what you require to find is the time taken. The reciprocal of 5/12 will give the desired result.
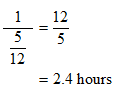
Comments for Problem Solving - Find the total time to paint a house
|
||
|
||
|
||
|
||


