Problem Solving - Measure out 7 liters of water

by Donna P.
(United States)

Question

Candice has an 11-liter can and a 5-liter can. How can she measure out exactly 7 liters of water into a third unmarked container?

Answer

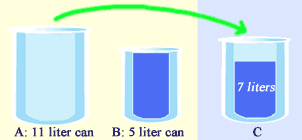
Let's label the 11-liter can as A, the 5-liter can as B and the unmarked container as C. These three cans are illustrated in the picture below: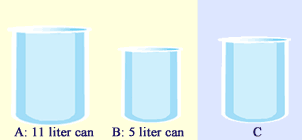

Now, to get 7 liters of water into container C, let's first fill up A to the brim. Obviously, now A has 11 liters of water in it. The picture below illustrates this.

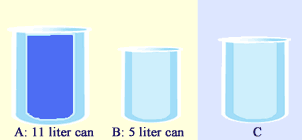
Next, pour the water from A into B and fill B with water to the brim. Now, B has 5 liters of water and A has 6 liters (11 - 5 = 6 liters) of water left in it. We can see that in the picture below:

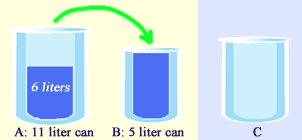
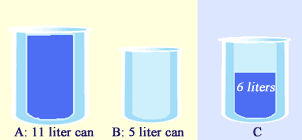
Alright, now we pour out all the water from A into C. Thus, now C has 6 liters of water as shown below.

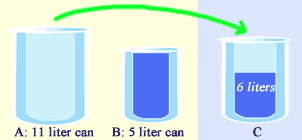
However, container C is still short of 1 liter of water. Hence, we need to find a water to get that 1 liter of water. Before we continue, let's pour away all the water in B and fill up A.

If we think carefully, we can get 1 liter of water by first pouring the water from A into B, as shown below.

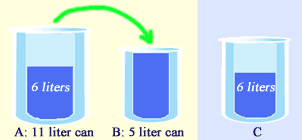
Now, A is left with 6 liters ( 11 -5 = 6 liters) of water. Next, let's pour away all the water in B.

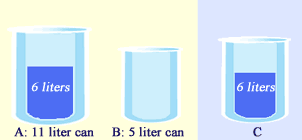
Again, pour the water from A into B. Now, A has 1 liter (6 -5 = 1 liter) of water left in it. Hooray! now we have that 1 liter of water.

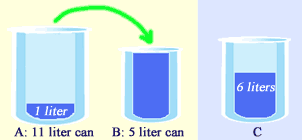
Final step, we pour that 1 liter of water from A into C. Now, C has total of 7 liters of water (6 +1 = 7 liters).

Alright, if you find quicker way to solve this, please feel free to post it in the comments section.