
Ratio of the volume and the surface area between two spheres
by Rabbani
Question
The radius of sphere A is twice that of a sphere B. Find the ratio among their surface areas and the ratio among their volumes.Answer
Consider the spheres below. These two spheres have the radius of 2r and r respectively.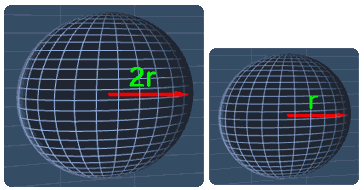
Sphere A Sphere B
The ratio of the surface area of sphere A to sphere B
Let the surface area of sphere A be SA and the surface area of sphere B be SB. Now we know that the formula for the surface area of sphere S is:
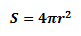
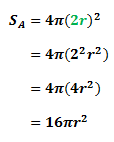
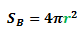
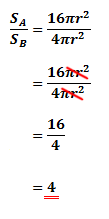
The ratio of the volume of sphere A to sphere B
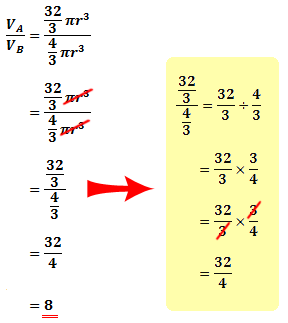
Let the volume of sphere A be VA and the volume of sphere B be VB. Now, we know that the formula for the volume of a sphere is:
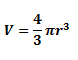
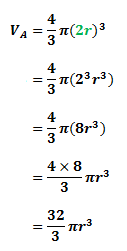
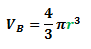
Hence, the ratio of VA to VB is:
Comments for Ratio of the volume and the surface area between two spheres
|
||
|
||
|
||


