2D Rotational Symmetry
Lesson Objective
This lesson shows you the ideas behind 2D rotational symmetry and you will get to see a quick video demonstration on it.
About This Lesson
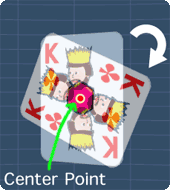
When we rotate a shape about its center point, we may notice that at a certain angle, the rotated shape coincides with its 'not rotated' self (see picture).
When this happens, the shape is said to have rotational symmetry. This lesson will show you the ideas behind it.
You can proceed by reading the study tips first or watch the math video. You can try out the practice questions after that.
Study Tips
Tip #1
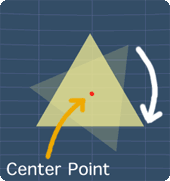
When we rotate the triangle about its center point for 360o, we will notice that it fits onto itself for 3 times for every 120o rotation.
By definition, the number of times a shape fits onto itself when rotated is called the order of symmetry.
Hence, we can see that the order of symmetry for this triangle is 3.
The math video below will show you more on this visually.
Tip #2
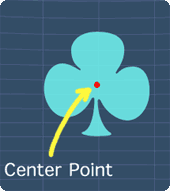
Now, this shape will only fits onto itself for 1 time after it is been rotated for 360o. Hence, the order of symmetry is 1.
However, for any shape that has rotation symmetry of order 1, that shape is considered as not having any rotational symmetry.
Hence, this shape has no rotational symmetry.
Now, watch the following math video to learn more.
Math Video
Click play to watch video
Sponsored Links
Math Video Transcript
00:00:03.100
This is a quick demonstration on two-dimensional rotational symmetry.
00:00:08.150
Now, let's consider this card. when I rotate this card about this point, for 360 degrees, observe how many times this card fits onto itself.
00:00:20.060
Let's start. One. Two.
00:00:29.180
So, we can see that, the card fits onto itself for 2 times.
00:00:35.080
Hence, with this observation, we can say that this card has rotation symmetry of order, 2.
00:00:43.020
Alright, let's take another example. Consider this flower.
00:00:48.100
When I rotate this flower about this point, for 360 degrees, observe how many times this flower fits onto itself.
00:00:57.020
Let's start. one. two. three. four. five.
00:01:07.140
So, we can see that, the card fits onto itself for 5 times.
00:01:13.050
Hence, we can say that this flower has rotation symmetry of order, 5.
00:01:20.040
That is all for this lesson. Try out the practice question to further your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on 2d rotational symmetry or pick your choice of question below.
- Question 1 on rotational and order of symmetry
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


