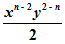Simplify the Expression: (2x^n/y^n)*(y/2x)^2

Question

Simplify (2x^n/y^n)*(y/2x)^2

Answer

STEP 1:   Observe the given expression: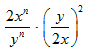If you observe the expression, then you notice that it contains a term in which a quotient is raised to a power. The first step in simplifying the expression will obviously be to simplify that term.

The exponent law which can be helpful for this purpose is:
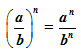
The law simply means to bring the power into each term of the quotient. See what happens when we apply this law.
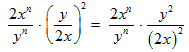
STEP 2:    The simplification of the term isn’t over yet. The denominator (2x)² can be rewritten using the law:

                                        (ab)ⁿ = aⁿbⁿ
Keep in mind that to raise a term to the second power means to multiply it by itself two times.STEP 3:    What we want to do here is to write as a product of quotients such that all expressions with like bases are brought together.
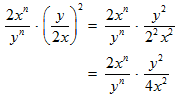
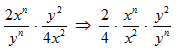
Since 4 goes evenly into 2, you cancel these numbers.
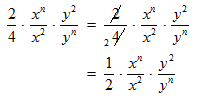
STEP 4:    Now, the operation left is to divide powers with like bases. When you divide, the exponents subtract.

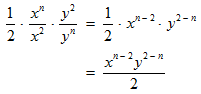
The final simplified expression that you get is: