Vertex of a Quadratic Equation

Lesson Objective

In this lesson, we will learn how to find the vertex of a quadratic equation.

Study Tips

Tip #1

The general quadratic equation is given as:

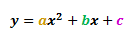
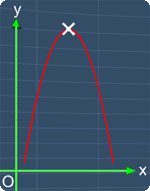
Where a, b and c are the coefficients of each term respectively. Now, the graph of a quadratic equation will always have a highest point or a lowest point depending on the value of a. This point is called the Vertex. The pictures below will illustrate this.

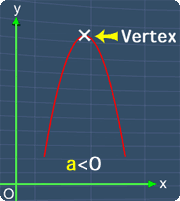
vertex is located at the highest point when 'a' is negative

Graph with a Highest Point

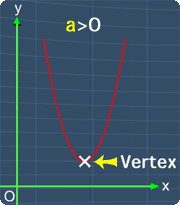
vertex is located at the lowest point when 'a' is positive

Graph with a Lowest Point

Tip #1 - Vertex Formula

The formula to find the x-coordinate of the vertex is shown below:

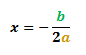
Where a and b are the coefficients in the general quadratic equation shown below:

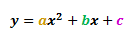
Math Video

Lesson Video

Sponsored Links

I'd Like to Contribute Using Paypal via MindBites.com

Math Video Transcript

00:00:04.130
In this lesson, we will learn about the vertex of a quadratic equation.

00:00:09.240
Now, this is the graph of the quadratic equation, y= -x^2 +2x.

00:00:17.160
Notice that, this is the highest point on the graph. Hence, this point is the vertex of a quadratic equation.

00:00:27.000
Also, if you have a quadratic graph as shown here, the lowest point, is also the vertex of the quadratic equation, y = 2x^2 -8x +3.

00:00:38.160
Now, there is a formula to calculate the x-coordinate of the vertex of a quadratic equation.  

00:00:44.090
The formula is, x = -b/2a. Now, what are 'a' and 'b'? Let's find out.

00:00:54.010
The general equation of a quadratic equation is given as, y = ax^2 +bx, +c. Where, 'a', 'b' and 'c' are the coefficients for each term respectively.

00:01:10.140
Let's see an example on using this formula, by using this equation, y = 2x^2 -8x +3.  

00:01:20.180
To find out the values of 'a', 'b' and 'c', we can rewrite this equation as, y = 2x^2 + (-8)x +3.

00:01:32.200
By comparing this equation with the general equation, we can see that, 'a' is equals to 2, 'b' is equals to -8, and 'c' is equals to 3.

00:01:44.200
Knowing this, we can substitute 'b', with -8, and substitute 'a', with 2. Now, we can simplify this term.

00:01:57.000
This term is the same as, [-(-8)]/[2(2)]. Negative multiply bracket -8, gives 8. 2 multiply with 2, gives 4. 8 divide by 4, gives 2

00:02:17.090
Finally, we have x equals to 2. With this, we know that the vertex of the quadratic equation has the x-coordinate of 2.

00:02:27.220
Let's go back to the original equation. Now, we can use the x–coordinate to find the y-coordinate of the vertex.

00:02:38.060
To do so, we can substitute x with 2.  -8 multiply with 2, gives -16. Adding -16 with 3, gives -13.

00:02:53.150
Again, we can substitute x with 2. 2^2 is the same as, 2 multiply by 2. Which is equals to 4. Let’s write down this number.

00:03:08.100
Let's continue. 2 multiply with 4, gives 8. 8 minus 13, gives -5.  

00:03:20.170
Hence, the vertex has y-coordinate of -5. This y-coordinate is located here.

00:03:30.080
Hence, the vertex of the equation has the coordinates of (2, -5).

00:03:40.080
Let's see another example. Consider the quadratic equation, y = -x^2 +2x. The graph for this equation is shown here. 
	
00:03:54.170
Now, the vertex is located at the highest point on the graph. Let's find the coordinates of this vertex.

00:04:03.210
Again, we start with the formula for the x-coordinate of the vertex of a quadratic equation, x = -b/2a.

00:04:13.050
To find the values of 'a' and 'b', we can compare this equation with the general equation, y = ax^2 + bx +c.

00:04:24.230
For easier comparison, we can rewrite this quadratic equation as, y = -1x^2 +4x + 0. Hence, we can see that, 'a' is equals to -1, ‘b’ is equals to 2, and 'c' is equals to 0.

00:04:44.120
Knowing this, we can substitute 'b' with 2 and substitute 'a' with -1.

00:04:53.170
Let's simplify this term. Now, this term is the same as, -2/2(-1). 2 multiply by -1, gives -2. -2 divides by -2, gives 1. Hence, we have, x equals to 1.

00:05:19.130
With this, the vertex has the x-coordinate of 1. Let's change back to the original equation.

00:05:27.130
Now, we can use this x-coordinate to find the y-coordinate of the vertex.  Here’s how. Substitute x with 1. 2 multiply with 1, gives back 2.

00:05:43.240
Let's continue. Again, substitute x with 1. 1^2, is the same as, 1 multiply with 1. This gives 1. Let’s write this down.

00:06:01.170
Finally, -1 add with 2, gives 1.

00:06:07.000
Hence, the y-coordinate of the vertex is 1. This can be seen here.

00:06:15.070
Hence, the coordinates of the vertex of this quadratic equation is (1, 1).

00:06:24.010
That is all for this lesson. Try out the practice question to test your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on vertex of a quadratic equation or pick your choice of question below.

Question 1 on finding the vertex of a quadratic equation

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons