Volume of a Pyramid
Lesson Objective
In this lesson, we will learn about the volume of a pyramid.
About This Lesson
In this lesson, we will:
- Learn about the formula for the volume of a pyramid.
- See an example on using the formula to calculate a pyramid's volume.
- See another example on using the volume formula to find the height of a pyramid.
The study tips and math video below will explain more.

Study Tips
Tip #1
In the previous lesson, we learned that the volume of rectangular solid is wlh. Now, the volume of a pyramid is just one third of the rectangular solid's volume.
Hence, for a pyramid with width w, length l and height h, the volume, V of the pyramid will be:
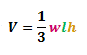
The math video below will provide more explanation on this formula and will show some examples on using it.
Math Video
Lesson Video
Sponsored Links
Volume of a Pyramid from MathExpression.com on Vimeo.
| |

You can contribute to the development of this site and keep it free by getting all six video lessons and volume of solids and calculator app for just US$1.99 from Apple App Store.
I'd like to contribute or to know more about the appMath Video Transcript
00:00:03.170
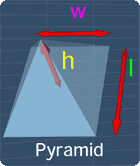
In this lesson, we will learn about the volume of a pyramid. Consider this pyramid.
00:00:15.090
Now, this pyramid has the width w, length l, and height h.
00:00:21.080
With this, the formula for the volume of this pyramid, V = 1/3(wlh).
00:00:29.180
Here, note that, 'wlh' is actually the volume of a rectangular solid.
00:00:36.190
Hence, the volume of a pyramid is actually one third of the volume of a rectangular solid.
00:00:43.190
Let's see some examples on how to use this formula.
00:00:47.160
This pyramid has the width 4cm, length 5cm, and height 3cm. Find its volume.
00:00:56.130
To find the volume, we use the formula for the volume of a pyramid, V equals to 1/3(wlh).
00:01:05.060
Now, since the width is given as 4cm, we can substitute w with 4. Similarly, since the length is given as 5cm. we can substitute l with 5.
00:01:18.090
Now, we can simplify by multiplying 4 with 5. This gives 20.
00:01:25.130
Next, since the height is given as 3cm, we can substitute h with 3
00:01:32.090
Let's continue to simplify by multiplying 20 with 3. This gives 60.
00:01:38.110
Alright, now we have 1/3(60).
00:01:43.100
Note that, this term is the same as, 1 bracket 60 over 3.
00:01:49.190
1 multiply by 60 gives back 60. Next, 60 divides by 3, gives 20.
00:01:58.210
Now, this number has no meaning unless we include the unit for it.
00:02:03.170
Since the units are given in centimeter, the unit for volume will be in cubic centimeter.
00:02:09.090
Hence, the volume of this pyramid is 20 cubic centimeter.
00:02:15.080
Next example, the volume of this pyramid is 10 cubic feet. Its width is 2ft, and length is 3ft. Find its height, h.
00:02:25.240
We can begin by using the formula for the volume, V = 1/3(wlh).
00:02:33.070
Here, since the volume, width, and length are given, we can find the height of the pyramid, h, by solving the equation for h. Here’s how.
00:02:43.150
First, note that, it is easier to work with this equation if we change 1/3(wlh), to the form of fraction, 1wlh, over 3.
00:02:55.120
1wlh is the same as, wlh.
00:03:01.020
Next, we can remove this fraction by multiplying both sides of the equation with 3.
00:03:06.240
This gives, 3V = wlh.
00:03:13.030
Now, since the volume is given as 10 ft, we can substitute V with 10. 3 multiply by 10, gives 30.
00:03:23.210
Since the width is given as 2 ft, we can substitute w with 2.
00:03:29.160
Similarly, since the length is given as 3 ft, we can substitute l with 3.
00:03:36.020
Here, we can simplify by multiplying 2 with 3. This gives 6.
00:03:42.230
Now, we have, 6h equals to 30.
00:03:47.190
Let's rewrite this equation, so that it looks neater.
00:03:52.230
Next, to find h, we need to remove 6.
00:03:57.130
To do so, we can divide both sides of the equation with 6.
00:04:02.160
This gives, h equals to 30 over 6. 30 divide by 6, gives 5.
00:04:11.150
Again, this number has no meaning unless we include the unit for it.
00:04:16.180
Since the volume is in cubic feet, the height of the pyramid will be in feet.
00:04:22.040
Hence, the height of this pyramid is 5ft.
00:04:27.020
This is all for this lesson. Try out the practice question to further your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on the volume of a pyramid or pick your choice of question below.
- Question 1 on finding the volume of a pyramid
- Question 2 on finding the height of a pyramid
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


