
Find the Area of a Triangle
Question
Find the area of a triangle whose vertices are defined by the points A(1, 3), B(–2, 1), and C(4, 2).
Answer
STEP 1: Construct the triangle using the given 3 coordinate points.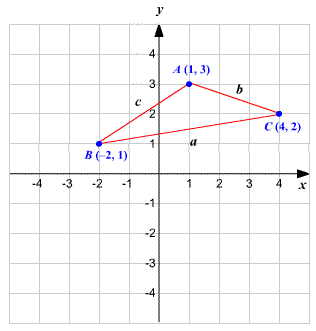
You have labeled the three sides of the triangle as a, b, and c. Since the coordinates of the three vertices are known, you can find the distance between these vertices using the distance formula.
Distance formula: If two points (x1, y1) and (x2, y2) are given, the distance between these points is given by the formula:
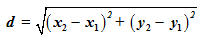
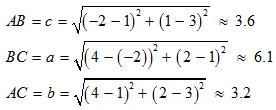
Now, you have obtained the lengths of the sides of the triangle. However, the height of the triangle cannot be determined. So, it is not possible to find the area of the triangle using the basic formula:
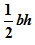
STEP 2: Recollect the Heron’s formula for triangles. The formula helps us to find the area of a triangle if all its sides are known.
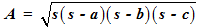
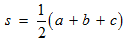
Substitute for the sides.
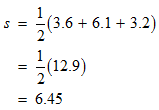
STEP 3: The final step is to replace all the variables in the Heron’s formula with the known values.
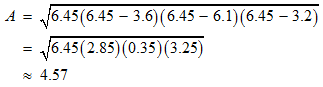
Comments for Find the Area of a Triangle
|
||
|
||
|
||


