How to Find the Volume of 3D Solids - The Basics
Lesson Objective
This lesson is an introduction to the basic ideas on how to find the volume of 3D solids. Here, we will be using a rectangular solid and a cylinder as examples.
About This Lesson
After familiarizing with surface area, it is time to learn about the volume of solids. As an introduction, we will be learning on how to find the volume of the following solids:
- Rectangular Solid
- Cylinder
Also, this lesson emphasizes on getting the unit for volume correctly.
The study tips and math video below will explain more.
Study Tips
Tip #1 - Rectangular Solid
To find the volume (V) of a rectangular solid, we just multiply the width (W), length (L) and height (H) of the solid together as shown below:
The math video below will explain this further...
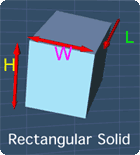
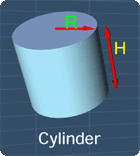
Tip #2 - Cylinder
Now, to find the volume (V) of a cylinder, you just need to multiply the area of the base (πR2) with the height (H) together. This formula is shown below:
The symbol, π, is just a number that is approximately equals to 22/7 or 3.142.
The math video below will explain this further...
Tip #3 - Unit for Volume
It is important to get the unit for volume correctly. Here are some pointers:
-
First, make sure all the units are the same
Let's say that the width, length and height of a rectangular solid are given as:
Width (W) = 20mm
Length (L) = 5cm
Height (H) = 3cm
Notice that the width has a different unit compared to the length and height? Now, we have to make these units the same by either changing all of them to mm or cm.
Since 10mm is equals to 1cm, 20mm must be equals to 2cm. Hence, we have:
Width (W) = 2cm
Length (L) = 5cm
Height (H) = 3cm
We can now calculate the volume since the units are now the same.
-
Next, understand what unit3 (cubic unit) means
Now, after ensuring the units are the same, we can calculate the volume, V below:
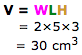
Notice the cm3 (cubic centimeter) above? This 'cubic' comes about because we multiplied the three lengths that are in cm. If W, L and H are in feet (ft), the unit for volume will be ft3 (cubic feet). Generally speaking, unit3 is the unit for volume where the unit can be mm, cm, m, feet, km, miles etc.
The math video below will explain this further...
Math Video
Lesson Video
Sponsored Links
| |

You can contribute to the development of this site and keep it free by getting all six video lessons and volume of solids and calculator app for just US$1.99 from Apple App Store.
I'd like to contribute or to know more about the appMath Video Transcript
00:00:03.200
In this lesson, we will learn the basics ideas on how to find the volume of solid.
00:00:09.080
To explain the basics, we will be using a rectangular solid, and a cylinder as examples.
00:00:16.080
Now, consider this rectangle with a width of W centimeter, and the length of L centimeter.
00:00:23.020
By now, we should know that the Area A, of this rectangle is W multiply L.
00:00:30.070
Since we are multiplying 2 lengths with unit centimeter, the unit for the area will be square centimeter.
00:00:37.090
Hence, the area of this rectangle is WL square centimeter.
00:00:43.220
Next, let's change this rectangle into a rectangular solid. Observe that, this rectangular solid now have a width of W centimeter, length of L centimeter, and the height of H centimeter.
00:00:58.170
Notice that, this solid is occupying certain amount of space, and the amount of space occupied is called Volume, V.
00:01:07.110
Now, how to find the volume of this rectangular solid? We just need to multiply the area. A, with the height, H.
00:01:17.000
Hence, by multiplying W, L and H, we get the volume of this rectangular solid as WLH.
00:01:26.080
Now, this volume WLH will only makes sense, if we include the unit for it.
00:01:32.140
Here's how. Since we are multiplying these 3 lengths with the unit centimeter together, the unit for this volume will be cubic centimeter.
00:01:41.240
Hence, the volume of this rectangular solid will be WLH cubic cm.
00:01:51.230
Next, let's learn on how to find the volume of a cylinder.
00:01:55.210
Consider this circle, with the radius R inches.
00:02:00.130
By now, we should know that the Area, A of this circle is PI r square.
00:02:06.100
Since the radius is in inches, the unit for the area of this circle will be square inch.
00:02:12.150
Hence, the area of this circle is pi r square, square inch.
00:02:19.190
Now, let's change the circle into a cylinder.
00:02:24.010
After doing so, this cylinder has the radius of R inches, and the height of H inches.
00:02:31.120
Notice that, this cylinder occupies certain amount of space. The amount of space occupied is the volume, V.
00:02:40.180
How to find the volume of this cylinder? To do so, we just need to multiply the area, A with the height, H. Hence, multiplying pi R square with H gives, pi R square H.
00:02:54.140
Now, this pi R square H only makes sense, if we include the unit for it.
00:03:00.160
Here's how. Since we are multiplying R square with H, notice that, this is actually multiplying 3 lengths with the unit inch together.
00:03:10.080
This will give the unit for this volume as, cubic inch.
00:03:15.140
Hence, the volume this cylinder will be πR2H cubic in.
00:03:21.110
That is all for this lesson. Try out the practice question to further your understanding.
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand this lesson better.
You can start by going through the series of questions on how to find the volume of solids or pick your choice of question below.
- Question 1 on how to find the volume of a rectangular solid
- Question 2 on how to find the volume of a cylinder
Site-Search and Q&A Library
Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.


