Improper Fractions and Mixed Fractions

Lesson Objective

In this lesson, we will learn about improper fractions and mixed fractions. Also, we will see how we can convert from improper to mixed fraction and vice versa.

Study Tips

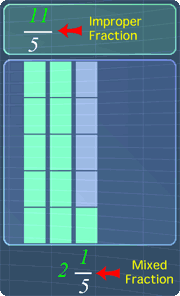
Tip #1 - Understand the difference

An improper fraction can be converted into a mixed fraction. Note that, these two fractions are equivalent. The only difference is at the way they are written. See the picture below:

$difference betweeen improper and mixed fractions$

The math video below will explain more about it.

Tip #2 - Improper to Mixed Fractions

To quickly convert an improper fraction to a mixed fraction, we can use the 'long division' method. The picture below shows an example on converting ¹¹/₅.

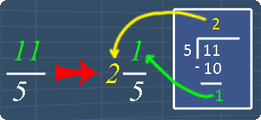
$converting improper to mixed fractions$

The math video below and the practice questions will explain this in detail.

Tip #3 - Mixed to Improper Fractions

To quickly convert a mixed fraction to an improper fraction, we use the steps shown in the picture below.

Below is an example on converting 2 ¹/₅.

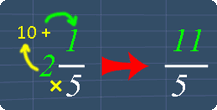
$converting mixed to improper fractions$

The math video below and the practice questions will explain this in detail.

Math Video

Lesson Video

Sponsored Links

Math Video Transcript

00:00:02.230
In this lesson, we will learn about improper fractions, and mixed fractions. 

00:00:08.150
Also, we will see how we can convert improper to mixed fraction, and vice versa.

00:00:17.080
Consider this fraction, 3 over 5.

00:00:21.240
Now, we can visually represent this fraction, with this long piece of bar.

00:00:28.030
Since the denominator is 5, we can divide this bar into 5 equal parts. 

00:00:34.100
Next, with the numerator as 3, 3 out of 5 parts can be colored green. 

00:00:40.080
Now, since the numerator is smaller than the denominator, this fraction is a proper fraction. 

00:00:47.060
Alright, let's increase the numerator from 3, 4,  5. 

00:00:52.230
Note that, from 5 onwards, this fraction is now considered as an I.F, because the numerator, is equals or greater than the denominator. 

00:01:03.060
Let's further increase the numerator of this improper fraction until 11.

00:01:09.060
Now, if we observe carefully, we can actually use these bars to convert this I.F, to M.F. 

00:01:16.210
Here's how.

00:01:18.170
Since, all the parts in this 2 bars are green, these bars can be considered as 2 whole green bars.

00:01:26.090
As for the remaining bar, we have 1 out of 5 part colored as green.

00:01:31.210
So here, is the mixed fraction 2, 1 over 5, converted from  I.F, 11 over 5.

00:01:39.230
As you can see, using these bars to convert I.F to M.F, is quite tedious.

00:01:46.210
Therefore, we need to learn a quicker way of doing this.

00:01:50.190
Here's how we can quickly convert the I.F, 11 over 5, to a M.F.

00:01:57.150
First, we know that 11 over 5 is the same as 11 divides 5. 

00:02:03.120
So, by doing the division, we get the quotient as 2, which is actually the whole number for the mixed fraction.

00:02:12.110
Next, 2 multiply by 5 gives 10. 11 minus 10 gives the remainder as 1.

00:02:20.120
This remainder, 1, becomes the mixed fraction numerator, and it is actually the green part here.

00:02:29.220
Here, we can see that, we had successfully converted this improper fraction to mixed fraction.

00:02:37.060
Next, let's convert this M.F back to I.F.

00:02:42.080
First, we multiply 5 with 2. This gives 10.

00:02:47.170
This multiplication is actually the same as, finding the 10 green colored parts here. 

00:02:54.190
Next, notice that, there is 1 more part to include.

00:02:59.170
We can include it by adding, 10 with 1. This gives 11, where it is actually the I.F's numerator.

00:03:09.100
Here, we had successfully done the conversion from M.F to I.F.

00:03:16.210
That is all for this lesson. Try out the practice question to test your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on improper fractions and mixed fractions or pick your choice of question below.

Question 1 on converting improper to mixed fractions
Question 2 on converting mixed to improper fractions

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons