Perimeter of a Parallelogram

Lesson Objective

In this lesson, we will see some examples on the perimeter of a parallelogram...

Study Tips

Tip #1

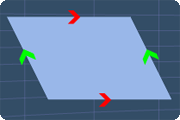
A parallelogram has two pairs of parallel sides and its opposite sides are equal in length. These properties are shown on the right.

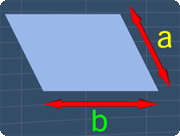
Now, if the parallelogram has sides of length a and b, the perimeter of the parallelogram, P, will be:

P = 2(a+b)

a parallelogram has 2 pairs of parallel sides

a parallelogram with side lengths of a and b

This formula is similar to the formula for the perimeter of a rectangle. Rather than repeating the same explanation, the math video below will show some examples on the perimeter of a parallelogram without using the formula.

Math Video

Lesson Video

Sponsored Links

Math Video Transcript

00:00:04.010
In this lesson, we will see some examples on the perimeter of a parallelogram.

00:00:09.220
Consider this parallelogram. We can see that, these 2 parallel sides have the length of 3cm and these 2 parallel sides have the length of 5cm.

00:00:24.030
Find the perimeter of this parallelogram.

00:00:28.070
Now, to find the perimeter of the parallelogram, P, we just add the length of these sides together.

00:00:36.110
Hence, we have P, equals to 3, add with 5, add with another 3, and add with another 5.

00:00:51.230
Therefore, we have P=3+5+3+5.

00:00:59.020
Let's calculate this. 3, add with 5, gives 8. 5, add with 8, gives 13. 3, add with 13, gives 16.

00:01:15.140
Hence, we have P=16.

00:01:20.120
Now, this number has no meaning, unless we include the unit for it.

00:01:26.070
Since the side lengths are given in centimeter, the perimeter must also be in centimeter.

00:01:32.210
Hence, the perimeter of this parallelogram is 16cm.

00:01:40.120
Next example, the perimeter of this parallelogram is 30ft. Find x.

00:01:50.040
Here, we can see that, this parallelogram has 2 parallel sides of length 8 feet, and, another 2 parallel sides of length x.

00:02:01.180
Now, we can find the perimeter of the parallelogram, by adding all the side lengths together.

00:02:08.240
By doing so, we have x, add with 8, add with another x, and add with another 8.

00:02:26.120
Since the perimeter is given as 30ft, this expression must be equals to, 30.

00:02:33.180
Before we continue, let's arrange the like terms together.

00:02:39.090
Now, let's simplify this equation. 8, add with 8, gives 16.  

00:02:48.040
x, add with x, gives 2x.

00:02:53.000
Now, we have 2x+16=30.

00:02:59.160
To get a step closer in finding x, we need to remove 16.

00:03:05.120
To do so, we add -16 to both sides of the equation.

00:03:11.010
By doing so, we get, 2x equals to, 30 minus 16. 30, minus 16, gives 14.  

00:03:24.170
Next, to find x, we need to remove 2. We can do so, by dividing both sides of the equation with 2.

00:03:36.170
By doing so, we get, x=14/2.

00:03:44.080
14, divided by 2, gives 7. Hence, we have, x=7.

00:03:55.010
Again, this number has no meaning unless we include the unit for it.

00:04:00.170
Since, the unit is in feet, 7 will also be in feet.

00:04:06.230
Finally, we have, x=7ft.

00:04:13.220
That is all for this lesson. Try out the practice question to further your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on the perimeter of a parallelogram or pick your choice of question below.

Question 1 on finding the perimeter of a parallelogram
Question 2 on finding side length of a parallelogram

Site-Search and Q&A Library

Please feel free to visit the Q&A Library. You can read the Q&As listed in any of the available categories such as Algebra, Graphs, Exponents and more. Also, you can submit math question, share or give comments there.

Share This Page

Back to Topic Lessons